소수란?
소수 : 자기 자신과 1이외의 어떤 정수로도 나누어 지지 않는다.
즉, 2 ~ n-1 까지 나누려고 해도 나누어지지 않는 수이다.
1000이하의 소수 구하기

- n이 소수인지를 검사하기 위한 for문 하나.
- 1과 본인의 값(1000)을 제외한 값으로 나눠주기 위해 모든 수를 차례로 스캔하는 for문 하나
- 안쪽 for 문에서 하나라도 나눠지는 수가 있다면 반복문을 중단하고 다음 수로 넘어간다.
- 나눠지는 수가 하나도 없다고 하면 마지막에는 결국 스캔한 값이랑 같아지게 되므로 i == j 조건을 추가 하여 출력해준다.
- 이 조건문은 안쪽 for문을 나왔을 때도 검사가 가능해야 하므로 for문의 초기화를 위한 선언은 for문 밖에서 정의 해준다.
위의 소수구하는 식의 문제점
- 1.n이 2또는 3으로 나누어 떨어지지 않으면 그의 곱인 6으로도 나누어 떨어지지 않는다.
- 따라서 불필요한 나눌셈을 진행하고 있는거나 마찬가지 이다.
- 그럼 조건식을 아래와 같이 변경 할 수 있다.
| 2부터 n-1까지의 어떤 소수로도 나누어 떨어지지 않는다. |
이를 이용하여 알고리즘을 개선함.
개선된 알고리즘으로 소수 구하기.
- 첫 요소의 값은 2로 초기화한다.
- 바깥쪽 for문은 3부터 시작하고 짝수를 제외한다.
- 안쪽 포문은 2부터 n-1까지의 어떤 소수로도 나누어 떨어지지 않는다. 를 고려한다.
- ptr은 현재까지 저장된 소수의 개수이다.
- i는 1부터 소수의 갯수까지만큼 for문을 돌린다.
- prime[i]는 소수의 갯수의 마지막 요소값까지 나타내준다.
- n에서 prime을 나눈 값이 나머지가 0이면 break; 어느것으로도 나누어지지 않고 for문을 빠져나오면
- ptr == i 조건을 만족하게 된다.
- 그러면 prime의 마지막 요소에 그 값을 저장해 준다.
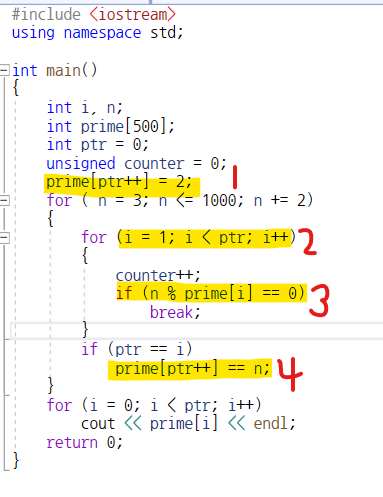
이 알고리즘의 문제점 : 2 * 50, 50 * 2.--> 굳이 안해야 할 계산을 한번 더 하고 잇따.
아래 그림처럼 제곱근을 한변으로 하는 이후의 직사각형에 대한 계산량을 줄여야한다.

소수 구하기의 더욱 개선된 알고리즘
안쪽 for문 조건 값 변경

'알고리즘' 카테고리의 다른 글
| [알고리즘] 선형검색 (0) | 2021.10.01 |
|---|---|
| [알고리즘] 구조체 (0) | 2021.09.30 |
| [알고리즘] 배열 요소 정렬 / 함수형식 매크로 (0) | 2021.09.29 |
| [알고리즘]난수사용하여 배열 요솟값 설정 및 최댓값 확인 (0) | 2021.09.29 |
| [알고리즘] 배열2 (0) | 2021.09.29 |